SHOP NOW FOR GEAR
Login
Join Rigging Lab

Vectors, Scalars, and Unit-less Values, Part 2

Written By: Lance Piatt

Excerpt from Rigging Lab Academy's Force Multipliers 
Video is at the bottom

I want to look at how we add vectors together. Previously, we discussed that if someone describes a displacement where they had two miles north and one mile east, we can add those together to get that endpoint. I want to look at that graphically now and give a few examples.

Figure A

All we did when we did that, if someone moves two miles north, and I represent that by a line that might be two units long in a direction north, and then they go one mile to the east, so I’ve made that line there the same length as half of this one, then we know that their finished position is here.

And it can be described by that vector that we can draw there, that resultant vector. So we said that was two and that was one. What we did then is, effectively, I’ve taken two separate vectors, this one running two north. And then the second part of that description, I’ve got the tail of my new vector, the tail and the tip. I’ve got the tail of that vector and put it at the tip of the first one to draw in here, one. And then when I add those together, they come up with this final vector that describes that overall displacement.

Figure B Figure C

Now, I’ve got a couple of really relevant examples on the next slide (Figure B-C). This first one I’m going to start with, it’s pretty similar to the one we discussed a minute ago, where we’ve got two overhead anchors with an anchor focal point where this rigging plate is. And then we’ve got our load suspended below at the bottom of this yellow rope. So this is sort of the reverse vector edition. I want to work out if I hang a particular load here, and I’m going to say that’s a mass of 100 kilograms, and as we said before, that means we’ve got a weight of one kilonewton, if I hang that off that system, how much am I going to have in the tension in each of these strands of rope?

Well, I can solve this graphically if I take this line here, I might just change colors to make it a bit clearer, change to red, if I take this line and continue it in a straight line through my rigging plate. And I’ll do the same with my blue rope here. And then I’m going to turn that into a parallelogram. I want this line here, you’ll see that I’ve got this V1 already pre-drawn, the V2, sorry, the V1, I can now add in here as well. And the triangle that we’ve got drawn, the side lengths of this triangle actually define the ratio of the forces that apply to each anchor. And what I’ve depicted with this triangle is I’ve drawn a scale where that’s 10 arbitrary units long, it’s the same size as that triangle. And then I just want to measure the relative lengths of each of these sides.

So I’ve just drawn a radius into there and I can count up that scale. I’ve measured it, and it’s actually 43. And I’ll do the same with the other one. I can radius that one in and I can count down from the bottom to see that one is 85. So the relative side lengths of this triangle tell us exactly the ratio of the tensions in each anchor leg for the load that we’re applying in tension to our loaded strand. So for our one kilonewton weight that we’re suspending here, I can rewrite that and say that we would have 0.43 kilonewtons in this leg and 0.85 kilonewtons in this leg.

Logically, that makes sense. If we imagine that system where everything is hanging, we can see that, well, this anchor should be taking most of the load because the load is almost suspended underneath it. And this one here, it’s effectively just acting as a redirection, pulling it sideways a little bit. So that, obviously, will bear less than what our blue anchor did.

A few more examples. This time, for each of these examples, I want to consider the position of this rigging plate between each of the people in each example. Is it going to be stationary or is it going to move?

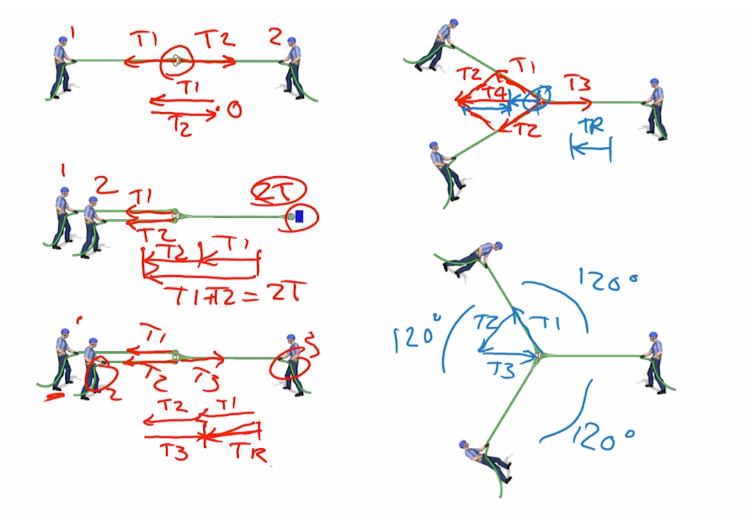
Let’s assume (figure 1) that each person can pull with the same amount of tension. And it doesn’t matter what length I choose, as long as when I’d represent this vector, it’s going to be an arbitrary length, and let’s draw it that long there. So this person here, person two, I’m going to say is pulling with tension T2. And this person one, is pulling with tension T1 in this direction. When I add those two vectors together, remember we said I get the first vector and I draw that in place, and then the second vector, I’m going to put the tip of the first to the tail of the second. And I’ll put them there in there, T1 and T2. And this gets us back to the start. So the resultant is zero and that anchor plate isn’t going to move at all. I work through these other examples as well.

Figure 1 Figure 2

This time (figure 2) we’ve got a fixed anchor and we’ve got two people, person one and person two. Person one’s applying T1, person two is applying T2. There’s T1. There’s T2. When I add those together, I draw T1 and then I’ll add T2 onto there. And the resultant that I get is actually that long, T1 plus T2. Let’s just call it 2T if each of those is pulling one unit of tension. So our anchor is going to feel two units of tension, which logically makes sense, but we’ve just demonstrated that by drawing the vectors and adding them.

What about this third one (figure 3), where we’ve got person one, person two, and person three? Person one is going to be pulling with T1, person two with T2, and person three with T3. I’ll add these three vectors together. T1 is there, T2 is there, and then T3 is coming back the other way. So the net result, if I start from the tail of my first vector and go to the tip of my third vector, we’ll call that TR for the T resultant. And logically, this makes sense as well because, effectively, we’ve got one person, this person will cancel out this person, so we’ve got one person applying all of the tension.

Figure 3 Figure 4

Let’s move to our fourth example (figure 4). And again, I’ll just draw these in quickly. We’ll call that T3, T1, and T2. They’re all roughly the same length. I’m going to do this over the top of the ropes that I’ve got drawn. So I’m going to add T2 to T1. And it’s that same parallelogram situation that I had before. So that is parallel to that, and that is parallel to that. I’ll add T1 and T2 to get a resultant in here, which we’ll call T4. And now you can see if I just change colors, if I then superimpose T3, or add that to T4, so that’s at length of T3, I’m left with this vector in here. So our resultant going from the tail where we started to the tip of where we finished is going to be that vector, which I’ll just draw out here as our resultant vector.
So the rigging plate will move to the left, but it will experience less tension than if just one person was pulling on it, for example.

Figure 5

The final example (figure 5), and looking at this, you should recognize that these angles here are about 120, which sort of rings bells for most of us as roping technicians. Everything should cancel out. Let’s check that by doing the vectors. So I’m going to have vector one coming up here, T1. Then I’m going to have my second one. So I’m going to draw that parallel to this T2 coming down here. Call that T2. And then this guy here is pulling that way with T3, which I can put in here, T3.So it finishes up back at the start again.

A couple of real-world photos from anchors that we set up at Smith Rock. I’m just going back to the red. I’ll just do these pretty quickly now that you’ve watched these examples. So I’m just going to pick an arbitrary length on this yellow rope and we’ll say we’ll go to there. And now I’m going to extend this rope through the anchor plate, and I’ll do the same with this one, extending through there. Now, this parallelogram, I want to construct so that it comes into this point here. So I’m going to draw one line there and one line there.
Figure 6

So if I call this length here (figure 6), 100, and this is now where we can start to put in some estimates because as long as we’re within 10 or 20%, that’s good enough for what we’re doing in the field. Looking at these two here, I would say, and if I radius this around here, that looks like about 60. And if I take this one around here, that looks like about 75. So what does that mean? This anchor running back this way is going to take 60% of the load, and this one up here is going to take 75% of the load.

We’ve got three more examples like that. Logically, we should be thinking with this one that this anchor here is going to be taking most of that load because it’s almost in line and this one is just pulling a little bit to the side, but let’s do our checks. So I’ll extend this line through the anchor and I’ll extend this line through the anchor. I’ll choose my arbitrary length as 100% at the base of the knot. And I want to draw this line parallel to this one here. That’s pretty close. And the same thing with this one.

Figure 7

So if this is 100 (figure 7), how long is that one there? If that was 50 there, then that looks like that’s about 35. And this one here looks like it’s about 80. So that means that this anchor, and logically, we sort of worked that out before, that takes about 80%, and this takes about 35%.

Figure 8

Next one (figure 8), a little bit quicker this time, extend this one through the anchor focal point and this one as well. Our knot is our endpoint. Draw parallel to this line here. And the same thing parallel to this line. I’ll just analyze one side of this triangle. I’ll radius this one in. That looks like about 60, and this one looks like about 80.

So 80% on this anchor and 60% on this anchor. That one might be anywhere between 65 and 90 and this one might be between 40 and 70. That’s near enough. The last one that we’ll do should be setting off some warning bells for that really large angle between these two, but let’s see what it tells us. So running through the anchor here and here. My arbitrary 100, I’m going to put at the base of the knot there. It could be anywhere. It could be out here or it could be in here, but let’s go there.

Figure 9

I’ll try and get these lines parallel. And this guy here. Okay. So now we can see that if that’s 100 in the middle, when I radius this around, it looks like it’s about 125. And then the same with this one. Bring that into the line of the yellow rope. So from here to here, that looks like about 120. So that tells us that this anchor here is taking 120% of the applied load and this one here is taking 125% of the applied load.
Figure 10

So this is all well and good if we can get above and take a photo, and use some really fancy apps that you can get like RigRite (it’s a really cool app for working your stuff out in the field if you’ve got a smartphone and can take a photo). But look, to be honest, we’re often in places where we don’t want to rely on the technology to do that. So here’s a quick and dirty way that we can do it in the field (figure 10).

Figure 11 Figure 12 Figure 13
Figure 14 Figure 15 Figure 16

So all I’ve got is a short sling (Figure 11-12) that I’ve started from the base of the knot to the anchor focal point there.

And then in the next slide, you’ll just see that I’ve spun that sling around (Figure 13).

So I’ve got my reference length of 100, and I’ve moved that around on a radius until that is parallel with one of our anchor legs. Okay. So now that lets me visualize the situation where I can draw a line in the dirt, or I can put a stick there and continue this one through to where it hits my sling.

And now I’ve got my three sides of my triangle (Figure 14-15). And I can see straight away that has hit about halfway along the length of that, which means that this anchor here is going to take 50% of the load. And while I’m just holding my sling there, I can see similarly that this one, the longer one, looks like it’s about 65% (Figure 16). So that’s going to take 65% of the load.

So whether it’s using a sling or a pen or a twig that you can break when you pick it up off the ground or just draw the lines in the dirt underneath the anchor, it’s a really speedy way to work out what your relative load distribution on your anchor points is with a particular applied loan.

 

Peace on your Days

Lance
Categories

About The Author:

Lance Piatt

Lance Piatt

Beginning his career in the rescue and rigging world as a “blue collar” SAR member with Deschutes and Jefferson County teams. Lance Piatt owns and operates Red Ibex Solutions, a sales and marketing wheelhouse blending rope rigging education and exquisite imagery with equipment knowledge and understanding; housing Rigging Lab Academy and Rescue Response Gear… Lance is producing high-end video education, working with several experts and instructors to produce unique series of “how to videos” and courses for rope rigging: Such as; the first ever full-length rescue training DVD, 'Tower Rescue', released in fall of 2005. As well as a series of scenario-based rescues ranging from cave rescue to cliff rescue.

218 thoughts on “Vectors, Scalars, and Unit-less Values, Part 2”

  1. buy instagram auto likes uk

    Thank you for another fantastic article. Where else may just anyone get that kind of
    info in such a perfect approach of writing? I have a presentation subsequent week,
    and I’m on the look for such information.

  4. Israel night club

    Nice post. I learn something totally new and challenging on sites I stumbleupon everyday. It will always be helpful to read articles from other writers and use something from other sites.

  29. Google seo

    Very great post. I simply stumbled upon your weblog and wished
    to say that I’ve truly loved surfing around your blog posts.
    In any case I will be subscribing in your rss feed and I hope you write
    once more very soon!

  33. שירותי ליווי בתל אביב

    וכך, בעשור האחרון התפתחה לה נישה
    חדשה בעולם העיצוב – קליניקות ומרפאות ייחודיות, הנשענות על עוגנים פסיכולוגיים, חברתיים וטיפוליים, מעבר להיבטים האדריכליים והתכנוניים.
    קליניקות מאובזרות, מרווחות ומוארות במיוחד.
    או מגע מלטף ועדין שיעניק לכם תחושה מרגיעה?
    עם זאת, ישנם עיסויים במרכז המתבצעים כעיסויים “יבשים” – כאלו
    המבוססים אך ורק על מגע המעסה.
    מסאג מפנק עם צעירה שובבה, לשעות ללא מעצורים.
    אם אתה מחפש נערת ליווי 18xil הוא המקום להתחיל את החיפוש אחר עיסוי מפנק.
    בדומה למה שאתם בודאי מכירים מטיפולי ספא בחיפה והסביבה אחרים
    (כמו עיסוי שוודי קלאסי / עיסוי באבנים חמות
    / עיסוי ארומטי ועוד), גם בטיפול רפואי, יהיה גוף המטופל מכוסה
    כמעט כולו במגבת או סדין, והמטפל יחשוף כל פעם אזור
    אחר בגופו של המטופל, הרלוונטי לאותו שלב בטיפול.
    עיסוי קלאסי בחדרה באזורים,
    תשומת לב רבה יותר מוקדשת לחלקים מסוימים
    בגוף (למשל ישבן, גב, אזור צווארון).
    ביקור במקום לפני הטיפול: אם אתם רוצים להיות בטוחים במאה אחוז בתמצאו מקום שעושה עיסוי ארוטי
    בראש העין שעונה על הדרישות שלכם,
    אנו ממליצים להתחיל בשיחת טלפון ולשאול
    על טיפולי העיסוי, על ההסמכות של
    המטפלים ומה הם בעצם מציעים. מדובר על מעין “כרטיסיית עיסויים בראש העין!”
    שאתם רוכשים מראש, כך שתוכלו לקבוע עם המעסה מפעם לפעם בהתאם ללוח הזמנים שלכם ולצרכים שלכם.

  50. บาคาร่า

    What you posted made a great deal of sense. However, think about this, suppose you typed
    a catchier post title? I am not suggesting your content is
    not solid, but what if you added something to possibly
    grab a person’s attention? I mean Vectors, Scalars, and Unit-less Values,
    Part 2 | Rigging Lab Academy is kinda plain. You should peek
    at Yahoo’s front page and see how they create news headlines to grab
    people to open the links. You might try adding a video or
    a pic or two to grab people excited about everything’ve written. In my opinion, it would bring your website a little
    livelier.

  51. Instagram followers

    hello there and thank you for your information – I have definitely picked up anything new from right here.
    I did however expertise some technical issues using this web site,
    since I experienced to reload the web site a lot of
    times previous to I could get it to load correctly.
    I had been wondering if your web host is OK? Not that I’m complaining,
    but sluggish loading instances times will often affect your placement in google and could damage your
    quality score if advertising and marketing with Adwords.
    Well I’m adding this RSS to my email and could look out for a lot more of your respective fascinating content.
    Ensure that you update this again soon.

  53. Lois

    A person essentially lend a hand to make severely articles I would state.
    That is the first time I frequented your website page and
    up to now? I amazed with the research you made to
    create this particular submit amazing. Excellent job!

  56. sexy

    Excellent goods from you, man. I have take into accout your
    stuff previous to and you are simply extremely excellent.
    I really like what you’ve obtained here, really like
    what you’re stating and the way in which by which
    you are saying it. You make it entertaining and you continue to
    care for to stay it wise. I can not wait to read much more from you.
    That is actually a wonderful web site.

  60. Dawna

    Howdy! Someone in my Myspace group shared this website with us so I came to look it over.
    I’m definitely enjoying the information. I’m bookmarking and will be tweeting this to my followers!
    Exceptional blog and great design and style.

  62. Richelle

    It’s awesome to pay a visit this website and reading the views of
    all friends about this paragraph, while I am also eager of getting know-how.

  69. gizmoxxx.com

    My programmmer is trying to persuade mee too move too
    .net from PHP. I have always disliked the idea ecause of the costs.
    Buut he’s tryiong none the less. I’ve beeen using
    WordPress oon varikus websites for abiut a year andd am nervous about switching to another platform.
    I have heard goo things about blogengine.net.
    Is thee a way I can import alll myy wordpress content int it?

    Anyy kind off helkp woud bbe really appreciated!

  77. Payoria

    If you re currently receiving chemotherapy for cancer, ask your oncologist cancer doctor when you can safely inject is cialis generic Methods A literature review was performed to identify all published randomized double-blind, placebo-controlled trials of tadalafil 5 mg once-daily for the treatment of LUTS and ED

  82. 토토사이트

    My spouse and I stumbled over here from a different page and thought I might check things out.
    I like what I see so i am just following you.

    Look forward to looking at your web page repeatedly.

  90. onlinemarketingservices81693.blogtov.com

    hello there and thank you for your info – I’ve certainly picked up anything
    new from right here. I did however expertise some technical points using
    this website, since I experienced to reload the web site a lot
    of times previous to I could get it to load properly. I had
    been wondering if your hosting is OK? Not that I’m complaining, but sluggish
    loading instances times will often affect your placement in google and
    could damage your quality score if advertising and marketing with Adwords.
    Well I am adding this RSS to my email and
    could look out for a lot more of your respective exciting
    content. Make sure you update this again very soon.

  95. Iva

    Its such as you read my mind! You appear to understand so
    much approximately this, like you wrote the ebook in it or something.
    I feel that you just could do with some % to pressure the message home a little
    bit, however other than that, this is magnificent blog.
    A fantastic read. I will certainly be back.

  100. online casino

    Thank you for some other informative blog. The place else may
    just I am getting that type of info written in such an ideal manner?
    I’ve a undertaking that I am just now working on, and I have been on the look out
    for such info.

  101. online casino

    I will right away grab your rss as I can’t to find your e-mail subscription link or
    e-newsletter service. Do you’ve any? Please let me understand so that I may just subscribe.

    Thanks.

  106. Julissa

    Hello There. I found your weblog using msn. That is a very neatly written article.
    I’ll make sure to bookmark it and come back to read more of your useful info.
    Thank you for the post. I’ll certainly return.

  107. Retinal Screening

    Magnificent items from you, man. I’ve consider your stuff previous to and you are simply
    too fantastic. I really like what you have received here, certainly like what you’re
    saying and the way wherein you say it. You’re making it enjoyable and you continue to care for to stay
    it sensible. I can’t wait to learn far more from you.
    This is really a great site.

  112. Towing software

    Hey there! Would you mind if I share your blog with my facebook group?
    There’s a lot of people that I think would really enjoy your content.
    Please let me know. Many thanks

  120. Pete

    Hi there, You’ve done a fantastic job. I’ll
    certainly digg it and personally recommend to my friends.
    I am sure they’ll be benefited from this website.

  127. click

    I was recommended this website by my cousin. I’m
    not sure whether this post is written by him as nobody else know such detailed about my trouble.
    You’re wonderful! Thanks!

  136. พีจีสล็อต

    Oh my goodness! Awesome article dude! Thanks, However I am
    experiencing problems with your RSS. I don’t know why I can’t subscribe to
    it. Is there anybody else having identical RSS problems?

    Anyone who knows the answer will you kindly
    respond? Thanks!!

  150. cutt.ly

    You made some really good points there. I checked on the internet for additional information about the issue and found most
    people will go along with your views on this site.

  154. paxtonnisk776.shutterfly.com

    I think everything said was very logical.
    However, think about this, suppose you added a little information? I am not suggesting your content isn’t good, but what if you
    added a post title to possibly get folk’s attention?
    I mean Vectors, Scalars, and Unit-less Values, Part
    2 | Rigging Lab Academy is kinda boring. You could
    look at Yahoo’s home page and see how they create post
    titles to get people to click. You might add a related video or a pic or
    two to grab people interested about everything’ve written. In my opinion, it would make your blog a little bit
    more interesting.

  157. fc2.com

    Hi this is kinda of off topic but I was wondering if blogs use
    WYSIWYG editors or if you have to manually code with HTML.
    I’m starting a blog soon but have no coding skills so I wanted
    to get guidance from someone with experience. Any help would be
    greatly appreciated!

  165. Worcester laser hair removal

    This is the perfect blog for everyone who wishes to understand this topic.
    You realize a whole lot its almost tough to argue with you
    (not that I personally would want to…HaHa).
    You definitely put a new spin on a topic that’s been written about
    for a long time. Excellent stuff, just wonderful!

  171. Camilla

    You really make it seem so easy together with your presentation but I in finding this topic
    to be actually something which I think I might never understand.
    It kind of feels too complex and very vast for me. I am taking a look forward to your next put up,
    I’ll attempt to get the hold of it!

  175. https://search-engine-ranking90862.mybjjblog.com

    I was wondering if you ever considered changing the page layout of your website?
    Its very well written; I love what youve got to
    say. But maybe you could a little more in the way of content
    so people could connect with it better. Youve got an awful lot of
    text for only having one or 2 pictures. Maybe you could space it out better?

  178. สล็อตpg

    Greetings from Colorado! I’m bored to tears at work
    so I decided to check out your website on my iphone during lunch break.
    I really like the information you provide here and can’t wait
    to take a look when I get home. I’m amazed at how fast your blog loaded on my phone ..

    I’m not even using WIFI, just 3G .. Anyways, fantastic site!

  189. DBA settlements

    I blog often and I really appreciate your content. Your article has
    truly peaked my interest. I am going to bookmark your blog
    and keep checking for new information about once per week.
    I subscribed to your RSS feed too.

  195. betflik

    When I initially commented I appear to have clicked the -Notify me when new comments
    are added- checkbox and from now on each time a comment is added I
    receive four emails with the same comment. Perhaps there is an easy method you can remove me
    from that service? Many thanks!

  196. porn

    Good post. I learn something totally new and challenging on blogs I stumbleupon every day. It’s always interesting to read content from other authors and practice a little something from their sites.

  204. Reinaldo

    Helpful information. Lucky me I found your website by
    chance, and I’m shocked why this coincidence didn’t came about in advance!

    I bookmarked it.

  205. Custom Louis Vuitton

    I must thank you for the efforts you have put
    in writing this blog. I am hoping to check out the same high-grade blog
    posts from you in the future as well. In fact, your creative
    writing abilities has inspired me to get my own site now 😉

  209. fc2.com

    I do not even understand how I ended up here, but I believed this post was
    once good. I do not know who you might be however definitely you’re going to a
    famous blogger if you happen to are not already. Cheers!

  211. Vonnie

    Hello There. I found your blog the use of msn. This is an extremely smartly written article.
    I will be sure to bookmark it and come back to learn extra of your helpful info.
    Thank you for the post. I will definitely return.

Comments are closed.

Helpful Links

Courses

Copyright (c) Red Ibex Solutions | Powered by Red Ibex Marketing Solutions

Privacy Policy