Vectors, Scalars, and Unit-less Values, Part 1

Written By: Lance Piatt

Full Video is at the bottom

A force multiplier is any factor or condition that contributes to the overall stress of a rope system during a dynamic state. Rating this dynamic state or rope movement/stress is best represented as the Dynamic System Safety Factor (DSSF). In other words, what’s our weakest link during the operation of our rope system at its point of greatest stress, typically during the onset of a hauling process.

During the course of this unit, we’ll examine five areas of misunderstanding in rope rigging commonly seen with emergency responders in the urban technical rescue environment:

Force Vectors
Tensile Force
Compression Force
Friction
And torque

The discussion will center around Unit-less Values, Scalars, and Vectors. These are essentially escalating terms and incorporate all the common aspects of we “think about” in terms of rigging a system. As you’ll see, there’s a lot going on!

So, I want to be really clear about the difference between unitless values, scalars and vectors.

Now, most people are already familiar with broadly what we mean by a vector, because we’re talking about resultant forces. But I need to just divide those three up a little bit. So unitless values are typically things like ratios. An example of a ratio is the mechanical advantage that we look at with systems. I don’t normally say that the mechanical advantage of that system is three-to-one feet, or three-to-one hours. It’s just three to one, we don’t have any units that we tack on the end of that description. So that’s a unitless value.

Another example of such a ratio is the number Pi, or something like 3.14159. We never put units on the end of that because it technically is the ratio between the diameter and the circumference of a circle. And whatever we measure that diameter in, centimeters, then we would put the Pi in there and we get an answer that’s in centimeters. So we don’t put a unit with the number Pi, because it is a ratio.

The next thing, if we do start to associate values, if we’re talking about measuring the length of things, so I can say to someone, “How long is that pen?” And then I can get a ruler and put it there and measure it. And I might get that that’s 15 centimeters. That unit on the end is important, because if I just said 15 and then wrote that down, it’s a pen that’s 15 long. Someone else might read that and say, “Well, is that centimeters or is it inches? Or … ” And they have to guess. So we’ve got to be quite specific when we’re measuring things like that, which is why we put units like centimeters.

So a scalar only has a dimensional unit that we associate with it. Vectors, now, are the next step in that process. When we measure vectors, we don’t just need to measure how many or how far or how long. We also need to say what direction, where we’re going to be applying that effort or that distance.

Now a good example, just to distinguish between a scalar value and a vector quantity is if we’re talking about traveling. So I can say that I’ve just traveled a distance of two miles. That would be a scalar measurement of distance. The vector equivalent of that, we would describe as displacement.

And if I want to talk about that as a displacement, I don’t just say I’ve traveled two miles, but I might say that I’ve traveled two miles heading due north. And that way, if I’ve got someone describing on a radio their journey, they might say they’ve gone two miles due north, and then they’ve gone one mile east. And that enables me to work out exactly where their position is because I can go up two miles and across one. And on the map, I can plot their position, which gives me a final vector displacement from here to this point.

So the vectors and that description of magnitude and direction are really important when we’re talking about analyzing the forces in the systems that we’re going to be working with.

Let’s consider one such system. And it might be a typical … If it’s a rope access context, a Y hang anchor, where we would have, and I’ll just go to the tablet here. I might have one anchor point in this position here, and I might have another anchor point here. And then I’m going to set up my roping system so that it’s attached to both of these anchors. I’ll have some connector or some knot system here. And then I might have my load suspended below on that rope based system.

When we’re working out our resultant forces and the way we distribute the loads, or attribute the amount of tension in each of these anchor legs as a result of this load being applied to the system, we’ve got directions that are actually defined by each of these anchor legs in the system.

Another example where we’re looking at forces is if I have an object at rest on a surface. So it might be a block of steel at rest on a nylon surface, for example. We spoke about weight before. That block of steel is exerting a downwards force on that surface that it’s resting on. It might, for argument’s sake, have a weight of one kilo-Newton, 220 pounds if it’s a static mass, or a hundred kilograms. If I want to move that block, I need to apply a force in a particular direction. And I might apply a force of 0.5 kilo-Newtons from behind the block to try and start moving that along.

Now, if I want to analyze what’s going to happen with that movement, I need to consider all the forces acting on that block. Another force is friction, and we’ll be talking a lot about friction as part of this series. So I can now consider that block … I’m going to be applying this external force from behind, I’ve got the weight here, and I’ve got the friction between those two surfaces. I need to consider all of those before I can start to work at how that’s going to move.

The other place where this will become significant is we look at the ratings of the equipment that we’re using as rope technicians. They’re typically rated in terms of kilo-Newtons, as either a working load limit or a safe working load, or an MBS. And we need to know how to interpret that stuff. If a carabiner is rated to 30 kilo-Newtons, we need to be able to work out, “What does that mean in terms of suspending a static mass from that carabiner?”

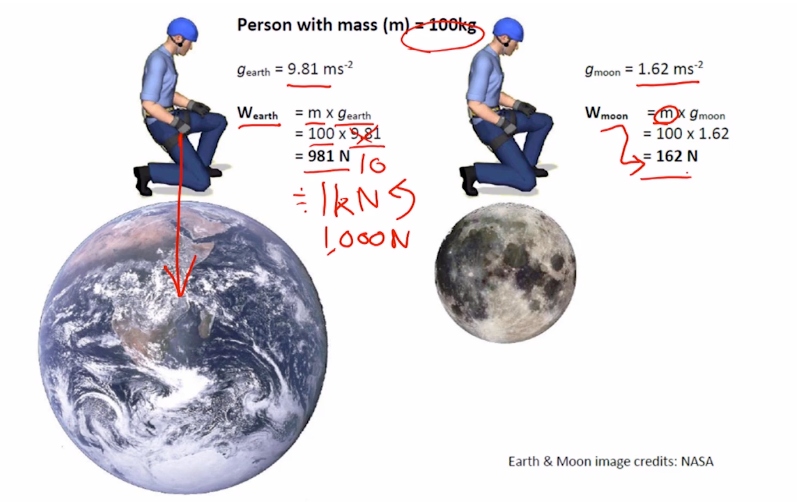
Here we are looking at weight and its relationship with mass, you might remember from school, force equals mass times acceleration. Now, how does that apply to weight? Well, weight is a force. And when we’ve got someone on the Earth, they’re subjected to the acceleration due to gravity on Earth, which is 9.81 meters per second squared. That’s the rate at which, if I drop something, it will accelerate towards the center of the Earth, if it’s unimpeded.

So if we consider a person with a mass of 100 kilograms, and they’re positioned on the Earth, their weight applied towards the center of the Earth, we can calculate by saying, “Weight equals mass times the acceleration due to gravity.” We know their mass is 100 kilograms, the acceleration due to gravity is 9.81 meters per second squared, so we come up with a weight of 981 Newtons.

Now those sort of numbers are hard to work with in the field, so typically we’ll make an approximation, and say rather than 9.81, let’s call that 10, which means then we can say that their weight is approximately equal to one kilo-Newton. I just did a little trick there, or a little sleight of hand. A thousand Newtons is the same as that one kilo-Newton.

Now just reinforcing that position that my mass stays the same, regardless of where I am, because mass is just a function of volume and density, if I take that same person and take them to the Moon … Their mass remains the same. However, the acceleration due to gravity on the moon is only 1.62 meters per second squared. So that means if I run these same calculations, the weight of that same person on the Moon is only 162 Newtons rather than a thousand Newtons. It’s less than a fifth. So the mass remains the same, but the weight is quite different.

So that consideration of forces, we’re going to move forwards with in every part of the next units that we’re looking at in this presentation: the force that we’re applying to static systems, and the forces that we’re going to be applying to dynamic systems.

Peace on your Days

Lance

About The Author:

Lance Piatt

Beginning his career in the rescue and rigging world as a “blue collar” SAR member with Deschutes and Jefferson County teams. Lance Piatt owns and operates Red Ibex Solutions, a sales and marketing wheelhouse blending rope rigging education and exquisite imagery with equipment knowledge and understanding; housing Rigging Lab Academy and Rescue Response Gear… Lance is producing high-end video education, working with several experts and instructors to produce unique series of “how to videos” and courses for rope rigging: Such as; the first ever full-length rescue training DVD, 'Tower Rescue', released in fall of 2005. As well as a series of scenario-based rescues ranging from cave rescue to cliff rescue.